神经网络解决偏微分方程的原理在于通过模拟人脑神经系统的结构和功能,利用大量神经元和连接权重来逼近微分方程的解。通过构建适当的神经网络结构,可以将其训练成能够映射输入与输出关系的近似解算器。这种方法在求解复杂偏微分方程时具有显著优势,特别是在求解高维度、非线性问题以及复杂边界条件的情况下表现突出。神经网络在求解偏微分方程方面的应用广泛,包括物理、工程、金融等领域,为实际问题提供了高效且灵活的解决方案。
本文目录导读:
偏微分方程是数学中的一个重要分支,广泛应用于物理、工程、计算机科学等领域,对于复杂的偏微分方程,传统的数值解法往往面临计算量大、精度难以保证等问题,近年来,随着深度学习的快速发展,神经网络在解决偏微分方程方面展现出巨大的潜力,为什么神经网络可以解偏微分方程?其背后的原理是什么?本文将就此展开讨论。
神经网络的原理
神经网络是一种模拟人脑神经元结构的计算模型,通过训练数据自动学习并优化参数,神经网络的基本单元是神经元,多个神经元通过连接权重进行连接,形成复杂的网络结构,在训练过程中,神经网络通过调整连接权重来最小化损失函数,从而实现对输入数据的映射或预测,神经网络的强大之处在于其可以自动提取输入数据中的特征,并学习这些特征之间的关系。
神经网络解偏微分方程的原理
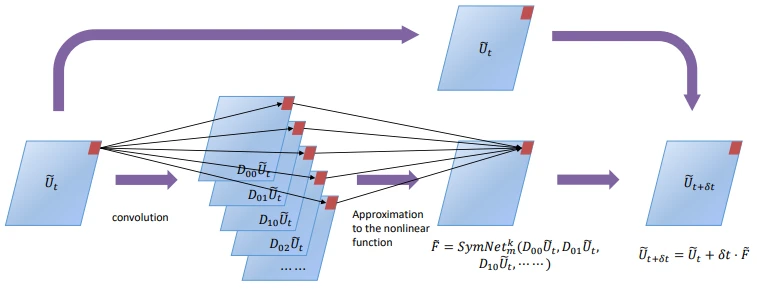
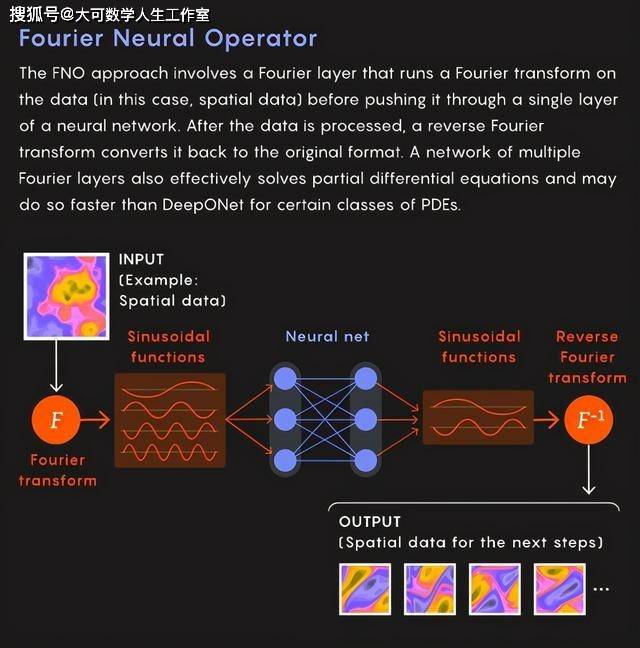
神经网络解偏微分方程的主要原理在于将偏微分方程的解表示为神经网络的一种输出,我们可以将偏微分方程的解空间看作是一个高维空间,而神经网络则可以近似这个高维空间中的函数,通过训练神经网络,我们可以找到这个近似函数,从而求解偏微分方程。
在神经网络解偏微分方程的方法中,常用的有两大类:一类是直接将偏微分方程的系数作为神经网络的输入,通过训练网络来逼近方程的解;另一类是将偏微分方程转化为一个优化问题,通过最小化某种损失函数来求解方程,这两种方法都利用了神经网络的非线性映射能力和优化能力,从而实现对偏微分方程的求解。
具体实现过程
在实际应用中,神经网络解偏微分方程的实现过程大致如下:
1、问题定义:需要明确所要解决的偏微分方程及其定义域、边界条件等。
2、数据准备:准备训练数据,包括方程的已知解、初始条件、边界条件等。
3、网络设计:设计合适的神经网络结构,如深度神经网络、卷积神经网络等。
4、训练过程:通过优化算法,如梯度下降法,对神经网络进行训练,使其能够逼近方程的解。
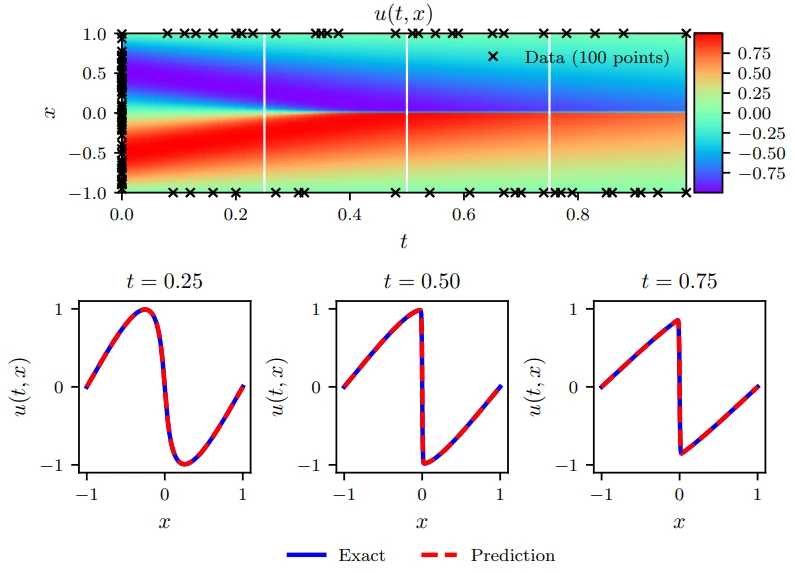
5、验证与测试:在测试集上验证神经网络的性能,评估求解精度。
优势与局限性
神经网络解偏微分方程的优势在于:
1、可以处理复杂的偏微分方程,特别是那些难以用传统方法求解的方程。
2、神经网络可以自动提取数据特征,无需人工设计特征提取方法。
3、神经网络的求解精度高,且可以并行计算,提高计算效率。
神经网络解偏微分方程也存在一定的局限性:
1、神经网络的训练需要大量的数据,对于缺乏数据的情况,效果可能不佳。
2、神经网络的训练过程可能受到初始化权重、优化算法等因素的影响,存在一定的不确定性。
3、对于某些特定的偏微分方程,可能需要特定的网络结构和方法,缺乏通用性。
神经网络解决偏微分方程的原理在于利用神经网络的非线性映射能力和优化能力来逼近方程的解,随着深度学习的不断发展,神经网络在解决偏微分方程方面的应用前景广阔,也需要认识到其存在的局限性和挑战,如数据依赖、训练不确定性等,需要进一步研究和发展更高效的神经网络结构和算法,以更好地解决偏微分方程。

 京ICP备11000001号
京ICP备11000001号